What are non-aromatic heterocycles?
Non-aromatic heterocycles can be related to open-chain analogous compounds, but the size of the ring may play a relevant role between them. The existence of a ring system imposes restrictions on the molecule that may be absent in the acyclic system.
The greater these constraints, the greater the difference between the two systems. Flexible molecules preferentially adopt conformations in which bonding interactions are maximized and repulsive non-bonding interactions are minimized.
In these conformations the bond angles and distances will be the “natural” ones. If the presence of a ring forces the molecule to adopt a structure in which it is not possible to achieve these preferred characteristics, the molecule can be considered to be “strained”.
However, it will preferably adopt a form that maximizes attractive or binding interactions, and minimize repulsive ones.
Ring strain in non-aromatic heterocycles can be considered as the sum of a number of factors:
- Angular strain of the bonds.
- Bond strain
- Bonding torsion
- Non-bonding interactions.
Somehow all these factors are interrelated and combining any one of them modifies the others.
Angular strain of the bonds
Distortions often occur in the “natural” angles of cyclic systems. The energy Vα required to distort the bond angle, with respect to its equilibrium value, is known as the “bond angle strain” or “Baeyer strain“. It is given by the following expression:
Vα = 0.01 (α-α0)2
Where α is the real value of the angle and α0 the natural value of the angle. A distortion of 10º has an associated energy contribution of 1 kcal/mol, 20º corresponds to 4 kcal/mol, and at 50º it is 25 kcal/mol.
Angular strain in small heterocycles
The largest distortions are found in the 3-membered rings. The saturated 3-membered rings have bond angles of 60°, which, when compared to the approximately 110° of a carbon with sp3 hybridization, corresponds to a large distortion. The distortion is even greater for unsaturated rings.
Table 1 below shows the stress corresponding to the 3-membered saturated rings (calculated on the basis of experimental and estimated formation enthalpies).
 | ∠CXC (º) | C—C (Å) | C—X (Å) | Strain (kcal/mol) |
| CH2 | 60 | 1.510 | 1.510 (1.54)* | 27.5 |
| NH | 60 | 1.481 | 1.475 (1.47) | 27.1 |
| CH3—SH | 48.5 | 1.492 | 1.819 (1.81) | 19.9 |
| CH3—OH | 61 | 1.472 | 1.436 (1.43) | 27.2 |
| *Average lengths of the unstrained system (sp3-sp3). | ||||
The effects of bond angle distortion are minimized in these small ring compounds due to changes in the hybridization of the atoms forming the rings.
For example, in saturated three-membered rings, the bonds that form the ring are not made up of sp3 hybrids, but have more “p” character, allowing a more effective overlapping of the orbitals directed outward from the axes that join the nuclei of the atoms of the ring.

The result is that the inter-orbital distortion is much smaller than the inter-nuclear angular distortion. Because, as the “p” character of the ring bonds increases, the “natural” inter-orbital angle decreases from 109.3º (sp3) -> 90º (p orthogonal).
The atoms of the ring can be considered to be joined by bent or banana-shaped bonds (bonding between σ and π) with a low charge density and directed outward from the ring.
This change in the ring bonds also affects other bonds, those bonding them to the substituents. These have a much larger “s” character than normal and the angles are larger.
Consequences of angular strain in small rings
- High reactivity and particularly easy opening.
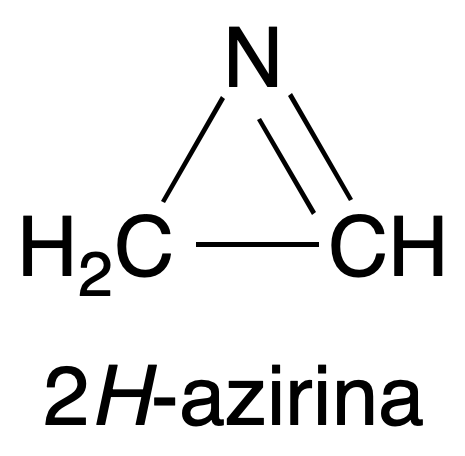
- Different spectroscopic properties. For example, the C=N bond strain frequency in the infrared (IR) spectrum of the 2H-azirine molecule, ν(C=N), increases to 1800 cm-1 compared to the normal value of 1650 cm-1 for unstressed imines.
- The distance between elements in oxiranes and aziridines is shorter than normal (conjugation transition), with more p-character, partial double bonding and π-orbital-p-ring overlap.
- The higher “s” character of the nitrogen orbital pair in aziridines, with respect to amines, makes it less basic than secondary aliphatic amines (with pKa = 8.04). In addition, the lone pair intercatalyzes less efficiently than in other amines with conjugative substituents, such as nitrogen bonded phenyl (basicity order: 4-membered heterocycles > 3-membered heterocycles).
- In aziridines, the rate of pyramidal inversion of nitrogen is considerably reduced (the barrier increases) compared to other nitrogen compounds:
fig-01
- Simple unstrained amines exhibit low nitrogen inversion barriers (ΔG‡ ≅ 6 kcal/mol), with the barrier in aziridine (ΔG‡ ≅ 17 kcal/mol) being much higher.
This is due to the higher angular strain in the flat transition state that is required for inversion. There is higher angular strain in the transition state and the inversion barrier is higher.
- The inversion barrier is also influenced by the nature of the nitrogen substituent.
Electron-withdrawing substituents, which stabilize the planar transition state, reduce the energy barrier.
There may also be a steric effect that destabilizes the pyramidal forms, e.g. the tertiary butyl group (tBut) lowers the barrier.
Angular strain in large rings
If we look at the 1-azabicyclo[3.3.3]undecane molecule, we can see that it has an almost planar arrangement of the groups at the nitrogen.
fig-02
Here, the effect is opposite to that observed in small rings. The angles are now larger than natural. Moreover, as the ring increases in size, this effect becomes more noticeable. The compound preferentially adopts a conformation in which the unshared electron pair of the nitrogen is directed toward the inside of the cage.
As a result, the molecule presents a great difficulty to protonate on the nitrogen on the outer side, resulting in a very weak base.
Torsional energy barriers
Bond torsion refers to the rotation around the axis joining two nuclei. The torsion angle or dihedral angle is the measure of the rotation of the bond with respect to the position at which the substituents of the nucleus are eclipsed.
In flexible systems, the energy of the molecule varies as the bond rotates.
Examples
- In the CH3-CH3 ethane molecule, the difference between the higher energy (eclipsed) and lower energy (alternating) forms is about 2.9 kcal/mol.
- The energy barrier for the two chair forms of cyclohexane is approximately 10.5 kcal/mol.
The chemical nature of such a barrier is complex and may contain contributions from the interaction of nuclei and unshared electron pairs of heteroatoms.
Single bonds
Saturated heterocycles contain C—X and in some cases X—X bonds as part of the ring system, for which the rotational barriers are different from those for C—C bonds.
C—X single bonds generally have lower rotational barriers than C—C bonds.
| Molecule | Energy (kcal/mol) |
| CH3—CH3 | 2.9 |
| CH3—NH2 | 2.0 |
| CH3—SH | 1.3 |
| CH3—OH | 1.1 |
X—X bonds, on the other hand, have much higher rotational barriers than C—C bonds.
Hydrazine example
Hydrazine (NH2—NH2) has a rotational barrier of 11.9 kcal/mol. This is mainly due to the unshared electron pair of nitrogens.
If we consider the rotational energy profile of hydrazine.
fig-03
The rotamer with the highest energy is the one in which the unshared electron pairs are eclipsed and the minimum when the electron pairs are at 90º.
The rotation barrier is lower for the confomer in which the unshared electron pairs are in trans (one relative to the other) arrangement.
Gauche effect
Heterocycles containing bonds show a preference for conformations in which the orbitals with unshared electron pairs are as perpendicular as possible.
A compound will be less stable if it is restricted to conformations in which the unshared electron pairs are eclipsed.
Diaziridinone example
- In the following monocyclic molecule, the substituents and electron pairs are in trans conformations, so this molecule is stable.
fig-04
- In the following bicyclic molecule, the substituents and electron pairs are eclipsed, and the molecule is therefore unstable. It rapidly loses carbon monoxide (CO) at a temperature of 25°C, and breaks down readily upon reaction with nucleophiles.
fig-05
Double bonds and partial double bonds
There are heterocycles that incorporate π-bonds in their structure. Bredt’s rule, formulated many years ago, prohibits the formation of double bonds on bridgeheads. Subsequent to its formulation, it was recognized that the stress criterion in such compounds was imposed by the size of the smallest ring presented by the trans olefin, and if this is large enough, it could exist (8-membered cycles of larger ones).
Thus, a few heterocycles with bridgehead C=N bonds are known, in which the groups attached to the π bond cannot be coplanar.
As a consequence these heterocycles are very reactive as illustrated in the figure below.
fig-05
Conformational preferences of saturated heterocycles
We have seen that the torsional energy of the C—X bond is lower than that of the C—C bond, while that of the X—X bond is higher.
These differences are very striking in flexible heterocycles, although other factors also influence the preferred conformation:
- Difference in C—X bond lengths compared to C—C bonds.
- Difference of Van der Waals radii.
- Presence of electrons on heterocycles.
The C—O bonds present values of 1.43 Å, and the C—N bonds values of 1.47 Å, much shorter than those of the C—Cbonds with values of 1.51 Å.
Van der Waals radii, also increase in the order: O < NH < CH2, with values of 1.4 < 1.5 < 2.0 Å, respectively.
Saturated 6-membered heterocycles
Just as cyclohexane and derivatives adopt the chair conformation, so do the 6-membered heterocycles.
The conformational energy barrier of ring inversion in tetrahydropyran is 9.9 kcal/mol. This value is very similar to that of cyclohexane, as it is also for other 6-membered heterocycles.
fig-06
If we consider the substituted heterocycle 3-methyl-1,3-dioxane:
fig-07
the A conformation, with the equatorial methyl, is even more favored than in methylcyclohexane (1.8 kcal/mol).
fig-08
This is because the shorter C—O bonds generate larger 1,3-diaxial interactions in B than in methylcyclohexane.
On the other hand, in the case of 5-methyl-1,3-dioxane in Figure:
fig-09
The A conformation is more stable but only by 0.8 kcal/mol. This is because in the B conformation the interactions of the methyl group with the unshared electron pairs of the oxygen are much smaller than the 1,3-diaxial interactions with the C—H bonds present in methylcyclohexane.
Piperidine and other nitrogen heterocycles undergo a more complicated set of conformational changes. Thus, there is, on the one hand, ring inversion and, on the other hand, tetrahedral inversion of the nitrogen substituents.
fig-10
This tetrahedral inversion in nitrogen is the lowest energy process.
The invertomer in which the nitrogen is equatorial is more stable. Moreover, the alkyl groups attached to the nitrogen also occupy equatorial positions and even more so in bicyclic systems.
fig-11
The A conformation is more stable than B, at 4.5 kcal/mol.
Nitrogen inversion barriers increase considerably when there are heteroatoms next to the ring heteroatom. These can come from inside or outside the ring.
fig-12
4- and 5-membered heterocycles
Cyclobutane is a non-planar molecule. The energy barrier for inversion is low, only 1.5 kcal/mol.
fig-13
For 4-membered heterocycles such as azetidine and oxetane, there are also similar, although lower, energy barriers.
fig-14
In oxetane the energy barrier is below the basal level of vibrational energy. Therefore, the molecule is planar as a consequence of the low torsional energy of the C—O bond.
The 5-membered heterocycles can be represented by a series of non-planar, freely interconverting structures, such as the so-called envelope structure or the half-chair.
fig-15
As in the case of other heterocycles, the torsional barriers are higher in the bonds attached to two heteroatoms and the rates of inversion of the tetrahedral nitrogen are reduced. Therefore, the molecules shown in the figure can be separated as diastereoisomers:
fig-16
Other types of interaction in saturated heterocycles
Anomeric effect
The presence of unshared electron pairs in heteroatoms of a heterocycle can have effects on the bonding system in other parts of the molecule. The anomeric effect is due to interactions of orbitals through bonding.
An orbital with the appropriate oriented electron pair can mix with bonding and anti-bonding orbitals of similar energy and affect the strength of those bonds.
An interaction of this type, is the one that takes place in the electron pair and an antiperiplanar σ bond of an adjacent atom.
fig-17
A strong interaction is possible due to the alignment of the electron pair with the σ bond. It can be represented by the following resonant structures:
fig-18
The electron pair can interact with both the σ orbital and the σ* orbital of C—Y. But if (Y) is electronegative the second interaction is more important.
The results are the transfer of electron pair electron density toward σ*, strengthening the C—X bond and weakening the C—Y bond.
If the interaction is stabilizing, the flexible molecules should preferably adopt conformations that maximize it.
Examples
In derivatives of tetrahydropyrans and other oxygenated and sulfur heterocycles, the electronegative groups (F, Cl, Br, OR) at the C-2 carbon tend to preferentially occupy the axial position, even though it is more sterically hindered.
It is called anomeric effect because it was first studied in monosaccharide chemistry, specifically in the anomeric equilibria of α and β-glycosides.
The anomeric effect is influenced by the presence of other substituents and also by the effect of the solvent.
fig-19
Solvents with a strong tendency to form hydrogen bonds also preferentially stabilize the equatorial alkoxy groups.
The effects on chemical reactivity are significant due to the interaction of electron pairs with antiperiplanar bonds.
fig-20
The A conformation is more resistant to hydrolysis than the B conformation, which has the axial aryloxy group.
The A conformation is not affected by 0.1 M HCl after several weeks at 39 ºC. However, the B conformation hydrolyzes rapidly under the same conditions in 7.7 min.
Engaging interactions through space
The simplest example of these interactions would be the hydrogen bonding that can occur.
For example, between a ring heteroatom and a hydroxyl substituent.
fig-21
The 3-hydroxyperidine molecule can exist in the A form with the hydroxyl in axial.
Another type of attractive interaction occurs in those compounds that present nucleophilic heteroatoms and electrophilic carbon atoms in the positions where they can interact.
The same occurs in open-chain compounds that have these two functions separated by a chain of 3 or 4 carbon atoms that can form a cycle.
fig-22
The same is true for the cycles. Several ring aminoketones preferentially adopt conformations that allow the nucleophilic nitrogen atom to approach an electrophilic carbon atom on the opposite side of the ring.
Examples
clivorin (alkaloid) in its crystal structure (X-ray), the nitrogen atom is abnormally close to the carbonyl group (1.99 Å) and is directed towards this group at the angle necessary for the incipient formation of a σ bond.
fig-23
The consequences are manifested in the simplest compounds of this group, e.g., the aminoketone in the figure:
fig-24
which is weakly basic and protonates on oxygen rather than nitrogen to give a bicyclic ammonium salt.
fig-25