Written by J.A. Dobado | Last Updated on 1 año
¿Qué son las propiedades coligativas de las disoluciones?
Cuando un soluto se disuelve en un disolvente se modifican algunas propiedades de este disolvente, tales como la presión de vapor, punto de ebullición, punto de fusión y la presión osmótica.
Índice
A estas propiedades se las conoce como propiedades coligativas. La extensión en la que se producen estas modificaciones dependerá tanto de la concentración como de la naturaleza del soluto. A continuación, se describen algunos ejemplos de propiedades coligativas más comunes de pendiendo del tipo de soluto que presente.
Disoluciones con componentes volátiles
Presión de vapor
Imaginemos que tenemos un líquido en un recipiente. Las moléculas de la superficie pueden abandonar la fase líquida y pasar a la fase vapor, situándose encima de los líquidos y ejerciendo una presión sobre estos denominada presión de vapor.
Cuando aumenta las moléculas en fase gaseosa aumentará la presión de vapor del líquido. Llegará un momento en que la presión de vapor se iguale a la presión atmosférica.
Pvap = Pat
Aparecerá un cambio de fase ya que se habrá alcanzado el punto de ebullición del líquido.
Si en lugar de tener un solo líquido en el recipiente tenemos una disolución binaria, pueden ocurrir dos cosas, que esta se comporte como disolución ideal o como no ideal, es decir, que se produzcan interacciones entre los dos líquidos.
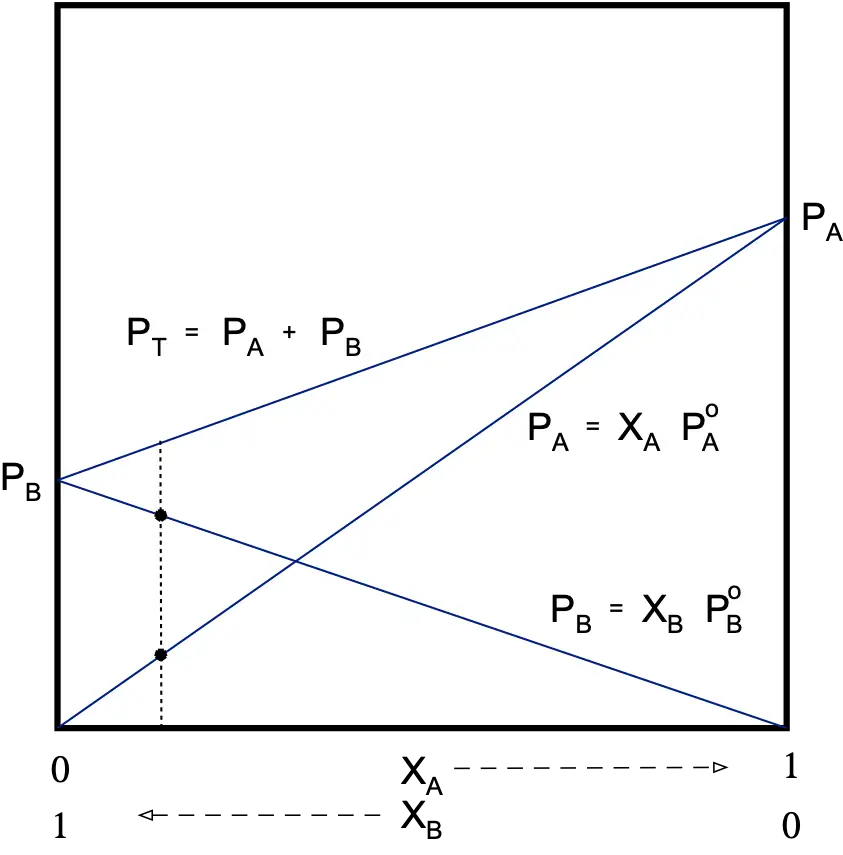
Disolución binaria ideal
Los componentes van a estar repartidos entre toda la masa de la disolución por igual, no existiendo interacciones ni atractivas ni repulsivas entre ambos, por lo que la tendencia a pasar a la fase vapor va a ser la misma en ambos. La presión total de vapor será igual a la suma de las presiones parciales de vapor de los componentes:
PT =PA + PB
Experimentalmente, se demuestra que una disolución ideal cumple la ley de Raoult:
PA =XA·PºA
PºA =presión de vapor del componente puro
XA = fracción molar
Por lo que:
PT =PA + PB = XA·PºA + XB·PºB
Se cumple que la presión de un componente en disolución es menor que cuando este componente se encuentra puro.
PA < PºA y PB < PºB
Esto indica que PT de la disolución estará siempre comprendida entre las presiones de vapor de los componentes que la forman.
A partir de las presiones de los componentes se pueden calcular las fracciones molares de los mismos:
PT =PA + PB = XA·PºA + XB·PºB
XA = 1 – XB
XB = 1 – XA
PT =PA + PB = XA·PºA + (1-XA)·PºB
PT = XA·PºA + PºB – XA·PºB = XA·(PºA – PºB) + PºB
XA = (PT-PºB)/ (PºA – PºB)
XB = (PT-PºA)/ (PºB – PºA)
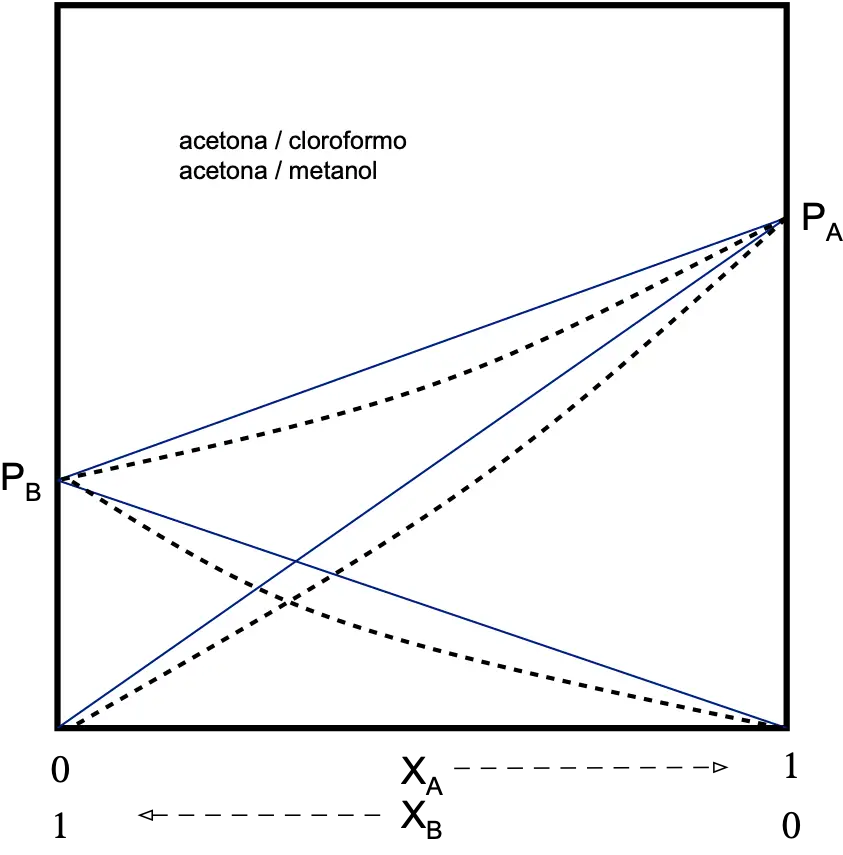
Disolución binaria no ideal
Pueden existir interacciones de dos tipos, atractivas o repulsivas.
Atractivas (desviación negativa)
La tendencia a escapar a la fase gaseosa será menor que la de una disolución ideal.
PA < XA·PºA
PB < XB·PºB
Por lo que la presión total de vapor de la disolución será menor que la prevista por la ley de Raoult.
PT < PRaoult
La desviación respecto a la ley de Raoult se mide con un coeficiente que se denomina “actividad” (γ). La actividad (γ) es igual a la presión real de un componente dividido por su presión teórica de la ley de Raoult.
γA=PA/XA·PºA γA ≤ 1 γB ≤ 1
Las disoluciones reales sólo tienen un comportamiento ideal cuando están muy diluidas. Los gases reales tienen un comportamiento ideal a bajas presiones y altas temperaturas.
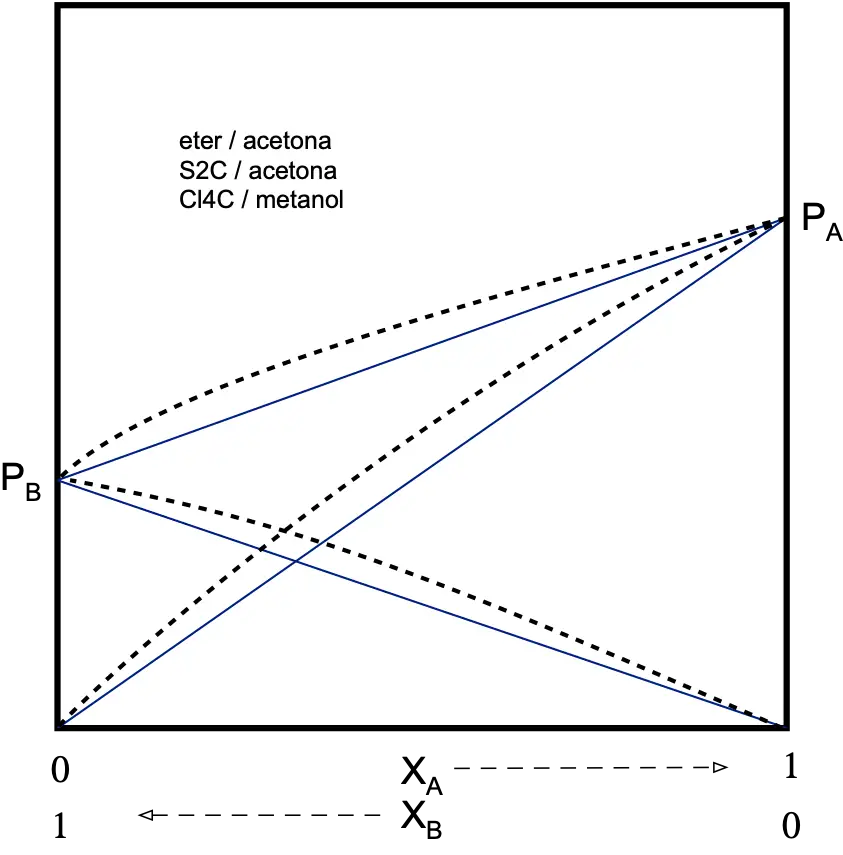
Repulsivas (desviación positiva)
Se va a producir una repulsión entre los componentes de la disolución por lo que la tendencia a escapar a la fase vapor será mayor que cuando se trata de una disolución ideal.
La PT de la disolución será mayor que la prevista por la ley de Raoult.
PA > XA·PºA
PB > XB·PºB
PT > PRaoult y γA ≥ 1 γB ≥ 1
Punto de ebullición
Temperatura a la que la presión de vapor (de una disolución en este caso) se hace igual a la presión externa.
Disolución binaria ideal
- Cuando la presión parcial del componente B sea mayor que la de A: PºB > PºA. El componente A será el menos volátil y estará menos presente en la fase gaseosa.
- En el caso contrario: PºA > PºB
El componente A será el más volátil y estará más presente en la fase gaseosa.
De forma que si aumentamos la presión, el vapor se enriquecerá en el componente más volátil y la disolución en el componente menos volátil, por lo que podremos separar ambos componentes.
En la práctica este sería un procedimiento dificultoso para separar ambos componentes, por lo que es más fácil aumentar la temperatura, ya que el componente que tiene una mayor presión de vapor posee una menor temperatura de ebullición. A este procedimiento se le llama destilación.
Disolución binaria no ideal
Las disoluciones que presentan interacciones atractivas o repulsivas no se pueden separar totalmente ambos componentes, por el procedimiento de la destilación.
Sólo uno de los componentes se podrá separar puro, quedando el otro mezclado con una composición definida denominada azeótropo.
En las disoluciones con interacciones atractivas el azeótropo presenta la máxima temperatura de ebullición superior a la de los componentes puros. En disolución con interacciones repulsivas el azeótropo tiene la mínima temperatura de ebullición, inferior a la de los componentes puros.
Mezclas de componentes inmiscibles
Al no existir una disolución entre ambos disolventes, cada componente conservará sus propiedades, por lo que la presión de vapor será la suma de las presiones de vapor de cada uno de los componentes puros.
PT = PA + PB = PºA + PºB
PT será mayor que cada una de las presiones parciales de los componentes de la mezcla:
PT > PºA PT > PºB
Y por tanto, la temperatura de ebullición de la mezcla será menor que las temperaturas de ebullición de cada uno de los componentes puros.
Ejemplo: Mezcla agua y aceite
Te H2O = 100 ºC
Te aceite = 350 ºC
Te total < 100 ºC
La presión de vapor de la mezcla y por tanto su temperatura de ebullición va a ser constante, ya que estas no dependen de las fracciones molares de los componentes.
El hecho de que la mezcla ebulla siempre a menor temperatura, se puede aprovechar para la destilación de componentes con altos puntos de ebullición.
Cuando se utiliza agua la técnica se denomina “arrastre por vapor de agua”.
Podemos ver la relación cuantitativa entre las presiones de cada uno de los componentes de la siguiente manera.
Según la Ley de Dalton:
Pi = Yi·P
para dos componentes la relación sería:
(Pºa / Pºa) = (Ya·Pt) / (Yb·Pt) ⇒
Pºa / Pºb = Yb / Yb = (na/nt) /(nb/nt) = na / nb = (ma/Ma) / (mb/Mb) ⇒
Siendo Ma la masa molar del compuesto a y Mb la masa molar del compuesto b.
Pºa / Pºb = (ma· Mb) / (mb ·Ma) ⇒
Ma =(ma· Pºb · Mb) / (mb · Pºa)
No se suele medir la «masa molar» a partir de presiones parciales, porque es muy costoso.
Por ejemplo: el nitrobenceno tiene un punto de ebullición 218.8 y densidad 1.0203 g/cm3. El Agua presenta un punto de ebullición 100 ºC y densidad 1.0 g/cm3.
Sin embargo, de la ecuación anterior se puede extraer otra expresión más útil. Así, nos permite relacionar las masas destiladas y son directamente proporcionales a las presiones de vapor y la masa molar de cada uno de los componentes.
(ma/mb) = (Pºa / Pºb) · (Ma / Mb)
Disoluciones con soluto no volatil
La presión de vapor total será debida únicamente a la presión parcial de vapor del disolvente.
PT = PD + PS = XD PºD + XS PºS (PºS = 0)
PT = XD PºD
Veremos las propiedades coligativas de estas disoluciones en condiciones ideales, es decir cuando se encuentren diluidas.
Presión de vapor
PT = XD PºD
Ya que la fracción molar del disolvente variará entre 0 y 1, tendremos que PºD > PT
Por consiguiente, el efecto de la adición de un soluto no volatil es el de reducir la presión de vapor del disolvente.
Se puede determinar el peso molecular de un soluto no volatil a partir de la presión de vapor de la disolución de la del disolvente puro:
PT = XD PºD = (1 – XS) PºD = PºD – XS PºD
XS = (PºD – PT)/PºD = ns/nt ≈ ns/nd (ns << nd en disoluciones diluidas)
(PºDn- PT)/PºD = mS·pmD/ mD·pmS
pmS = [PºD/(PºD – PT)] mS·pmD/ mD
Punto de ebullición
El punto de ebullición es la temperatura a la que la presión de vapor es igual a la presión atmosférica externa. Al añadir un soluto no volatil a una disolución aumenta la temperatura de ebullición de la disolución. Se produce una elevación del punto de ebullición del disolvente.
Este incremento de la temperatura de ebullición (ΔTe), se define como la diferencia entre el punto de ebullición de la disolución (Tes) y el punto de ebullición del disolvente puro (Ted):
ΔTe = Tes – Ted
Este incremento de la temperatura estará relacionado con la disminución de la presión de vapor de un disolvente al añadirle un soluto no volatil.
ΔP = PºD – PT
de forma que:
(PºD – PT)/ ΔTe = K ΔTe = (PºD – PT)/K
la elevación del punto de ebullición va a ser proporcional a la cantidad de soluto que se añada, o lo que es lo mismo a la fracción molar de soluto:
ΔTe = XS·(PºD/K) = XS · K’ XS = (PºD – PT)/PºD
también se puede relacionar el aumento del punto de ebullición con la molalidad:
XS = ns/nt » ns/nd = ns·pmD/mD (ns<<nd en disoluciones diluidas)
m = ns/(mD/1000) = 1000ns/mD
XS = m·pmD/1000
De esta forma
ΔTe = K’·XS = m·(pmD·K’/1000) = m Ke (Ke = cte ebulloscópica molal)
Ke se define como el aumento que experimenta la temperatura de ebullición del disolvente cuando este se hace 1 molal de soluto.
Podemos también relacionar el aumento ebulloscópico con el peso molecular del soluto:
ΔTe = m·Ke = (mS·1000/pmS·mD)·Ke
pmS = mS·1000·Ke/mD·ΔTe
Punto de congelación
El punto de congelación de un líquido puro es la temperatura a la cual el sólido y el líquido coexisten en equilibrio térmico. La presión de vapor del sólido y del líquido será la misma.
La adición de un soluto no volatil produce una disminución del punto de congelación del disolvente.
El descenso crioscópico es la diferencia de temperatura de congelación del disolvente puro y la de la disolución que contiene el soluto.
ΔTc = Tcd – Tcs
Donde Tcd es del disolvente puro y Tcs de la disolución con soluto. Por un razonamiento similar al seguido para el punto de ebullición concluiremos que:
ΔTc = m·Kc Kc = cte crioscópica molal
Kc se define como el descenso que experimenta la temperatura de congelación de un disolvente cuando esta se hace 1 molal de soluto.
De la misma forma podemos ver la relación que existe entre el descenso crioscópico (ΔTc) y el peso molecular del soluto (Ms):
MS = mS·1000·Kc/mD·ΔTc
Presión osmótica
La presión osmótica es una propiedad coligativa relacionada con la presión de vapor del disolvente.
Este fenómeno lo observo Abbe Nollet en 1748, relizando el siguiente experimento:
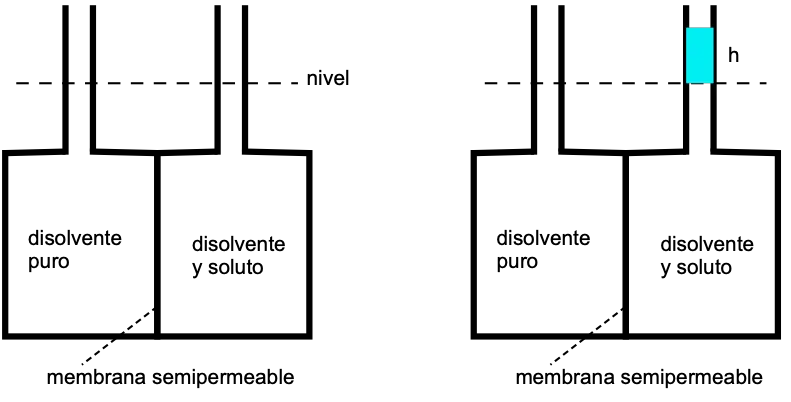
La membrana solo es permeable al disolvente, de forma que este la atraviesa en el sentido hacia donde haya menor concentración de disolvente, es decir, mayor concentración de soluto.
Esta diferencia de nivel es debida a la presión osmótica, que es la presión hidrostática que se opone a que el disolvente siga atravesando la membrana:
Π = h·ρ·g
h = diferencia de nivel entre los capilares
ρ = densidad
g = cte gravitatoria
- se demuestra que cuando la temperatura es cte, en disoluciones diluidas (ideales), la relación entre la presión osmótica y la concentración es constante.
Π/C = cte Π·V = cte
En 1885, van’t Hoff demostró que esta relación es similar a la de los gases ideales:
Π·V = n·R·T
- se puede relacionar también la presión osmótica con el peso molecular de la sustancia disuelta (soluto):
Π·V = nS·R·T = (mS/pmS)·RT
pmS = mS·RT/ Π·V
Disoluciones con electrolitos
Al estudiar las propiedades coligativas de las disoluciones se observa que un gran número de sustancias dan al disolverlas valores excepcionalmente elevados de estas propiedades que no pueden explicarse.
Estas disoluciones tienen como característica común que conducen la corriente eléctrica. Suelen ser ácidos, bases y sales, que reciben el nombre de electrolitos. Los valores elevados de sus propiedades coligativas sugieren que el número de partículas existentes en la disolución debe ser superior al de moléculas que se han disuelto.
van’t Hoff con el fin de mantener la validez de las ecuaciones utilizadas para el cálculo de las propiedades coligativas, estableció un factor empírico “i”, conocido como factor o coeficiente de van’t Hoff
i = (propiedad coligativa experimental)/(propiedad coligativa teórica)
así: i = Πexp/Πteo i = ΔTc(exp)/ ΔTc(teo)
por lo que para un electrolito:
Π = inRT/V ΔTc = imKc
se ha comprobado que en disoluciones diluidas, “i” suele adoptar un valor entero, 2, 3, 4, etc.
Cloruro sódico i = 2 NaCl
Cloruro cálcico i = 3 CaCl2
Cloruro férrico i = 4 FeCl3