Tabla de contenidos
¿Qué son las reacciones pericíclicas?
Las reacciones pericíclicas son reacciones concertadas en un sólo paso (por lo tanto no son reacciones radicalarias que implican varios pasos), y como indica su nombre se dan en un proceso en el que el estado de transición presenta un bucle cerrado de electrones interaccionantes, de tal modo que la forma de ese bucle implica unas características especiales de las distintas reacciones haciendo que unas reacciones se den y otras no, o bien haciendo que se de una cierta estereoquímica y no otra, esto implica que son estereoespecíficas (se obtiene sólo uno de los posibles estereoisómeros) por lo tanto en el estudio experimental se busca que las reacciones sean estereoespecíficas, si se encuentra que existe una cierta racemización, etc, se puede descartar totalmente un mecanismo pericíclico. El que transcurran en un sólo paso implica que no existen intermedios de reacción que se puedan estudiar, lo cual es un problema para su estudio experimental.
Vamos a desarrollar la teoría de Woodward y Hoffmann desde varios puntos de vista. Primero haremos un planteamiento de los aspectos teóricos donde vamos a tratar de predecir cuando se da una reacción determinada y con que estereoquímica. En un segundo paso tratarrmos experimentalmente de demostrar si existen o no reacciones pericíclicas de las distintas formas que introdujeron Woodward-Hoffmann.
Estas definiciones son:
- Reacciones de cicloadición: a partir de dos sistemas separados se forma un único sistema cíclico.
- Reacciones electrocíclicas: dentro de un mismo sistema se forma un sistema cíclico.
- Transposiciones sigmatrópicas: un grupo transpone a lo largo de un sistema π de electrones.
- Reacciones quelotrópicas: son reacciones de cicloadición en las que uno de los componentes es un sólo átomo.
- Reacciones de transferencia de grupos.
Son reacciones en las que todos los enlaces se forman y rompen en la misma extensión a lo largo de la coordenada de reacción, esto siempre ocurre así, en una reacción concertada, puede que un enlace siempre esté más formado, que el otro roto en el estado de transición, es decir que los estado de transición no tienen por qué ser simétricos o dicho de otra forma la reacción no tiene por qué ser sincrónica. El hecho de que sea concertada si quiere decir que se da en un sólo paso y los enlaces se rompen y se forman simultáneamente pero no sincrónicamente, por lo tanto en el estado de transición los enlaces que se forman pueden estar más formados que rotos los que se rompen. Esto ocurre siempre, así en las SN2 puede que el nucleófilo esté más unido al carbono que sufre la substitución que el enlace del grupo saliente roto.
Las definiciones hechas para los distintos tipos de reacciones pericíclicas son un poco arbitrarias, porque todas las reacciones pericíclicas se pueden considerar como un caso particular de cicloadiciones. Pero definamos primero las características fundamentales de estas distintas reacciones pericíclicas, su estereoquímica, etc., y después, veremos como las que no son reacciones de cicloadición, se podrán estudiar como casos particulares de reacciones de cicloadición.
Modelos teóricos para el estudio de las reacciones pericíclicas
Existen varias alternativas para realizar un estudio teórico de este tipo. Así tenemos el trabajo pionero de Woodward-Hoffmann, del que derivaron otros muchos y que abordaremos en último lugar. Primero veremos una alternativa más cualitativa pero que da buenos resultados.
La teoría de Woodward-Hoffmann trata de ver como se transforman los reactivos en los productos, e intenta predecir que cuando en la formación de los reactivos a productos la barrera de energía es grande entonces la reacción estará prohibida. Mientras que si esa transformación transcurre sin una barrera importante de energía, entonces estará permitida. Además, propusieron que para que se transformen los reactivos en productos, los orbitales que se correlacionan tienen que mantener la simetría orbitálica del sistema, es decir, al pasar de los reactivos a los productos la simetría del sistema tiene que mantenerse. A la puesta en práctica de esta correlación entre reactivos y productos se le denominan diagramas de correlación.
En primer lugar veremos un aspecto más cualitativo, teniendo en cuenta que en todas las reacciones pericíclicas se produce un estado de transición que está constituido fundamentalmente por una serie de electrones que interaccionan en un bucle cerrado y teniendo en cuenta que esto nos recuerda a los sistemas aromáticos donde además de la cadena σ, hay electrones π en un bucle cerrado. El número de electrones y su topología implica la aromaticidad o antiaromaticidad de los hidrocarburos cíclicos cerrados. El punto de vista de Dewar y Zimmerman, que fueron los que desarrollaron esta alternativa, es hacer una analogía entre el estado de transición y la aromaticidad o anti-aromaticidad de los hidrocarburos policíclicos poliinsaturados, de manera que si en esa analogía al estado de transición se le puede asignar un carácter aromático, este estado de transición estará estabilizado y por tanto la reacción estará permitida. Mientras que si en esta analogía al estado de transición se le puede asignar un carácter antiaromático, entonces el estado de transición estará desestabilizado y la reacción estará prohibida. Entonces se trata de construir un estado de transición aproximado que representa los pares de electrones que interaccionan en la reacción pericíclica y tratar de asignarle un carácter aromático o antiaromático.
Diagramas de interacción de orbitales
Para realizar la construcción cualitativa de este estado de transición se usan los diagramas de interacción, es decir, los estado de transición de las reacciones pericíclicas se construyen mediante estos diagramas que son una representación de la interacción de los orbitales que intervienen en la reacción pericíclica.
Algo de esto hemos visto ya al ver una reacción de cicloadición donde hemos puesto un sistema π de 2 electrones y otro de 4, hemos dicho que se debe de producir un ataque por arriba de tal forma que eso interacciona supra–supra.

Pero esto es sólo una interacción parcial que hay entre los componentes que intervienen.
Interacción supra o antara
Antes de llegar entre los tipos de interacción entre los componentes que intervienen que son los que fijan la estereoquímica de la reacción para poder analizar el diagrama de interacción en su conjunto es necesario analizar también la interacción dentro de cada componente. Es decir, tenemos que estudiar la interacción existente en un sistema π, dentro de un orbital σ, etc. Por ejemplo, si tenemos un sistema π de 2 electrones, puede interaccionar con otro supra o antarafacialmente, pero en ese sistema π de 2 electrones, en el estado de transición existe una interacción entre esos dos orbitales entre si de una forma que tiene que ser suprafacial.
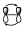
O bien, en un sistema de 4 electrones π, la interacción que hay dentro de esos orbitales será la que se muestra:
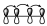
Esto nos indica que no existe interacción entre los extremos, pero si existe interacción dentro de los lóbulos de cada uno de ellos. Lógicamente, estos diagramas de interacción para ese sistema diénico tienen que ser equivalentes a este otro.
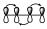
Puesto que la interacción de 2 lóbulos por arriba es equivalente a la interacción de estos por abajo. Hay que tener en cuenta que no nos estamos fijando en el signo de los distintos lóbulos, pero esos dos diagramas deben de ser equivalentes a la hora de analizar la interacción dentro de un sistema π.
Lo mismo que si tenemos un orbital s hemos visto que puede interaccionar con otros componentes de forma supra o antara, si lo hace supra los dos lóbulos del mismo signo interaccionan con otros, y viceversa. Pero la interacción entre sí lógicamente es de esta forma, puesto que forman el enlace

Por lo tanto, esa será la interacción que hay dentro de un enlace σ. Pero si nos fijamos en toda reacción donde interviene un sistema, normalmente ese sistema σ se convierte en un sistema π, en el estado de transición se está produciendo un cambio de hibridación sp3 a un orbital p, y por tanto no es ni una cosa ni otra, por lo que lo de arriba es equivalente a la interacción entre 2 orbitales p.

Es decir, que normalmente en los diagramas de interacción no se tiene en cuenta la forma que tienen los orbitales que forman parte, no se tiene en cuenta si es un orbital σ, si hay híbridos sp3 o sp2, etc, sino que se considera sólo los orbitales base que van a representar la interacción dentro del sistema. Un orbital σ se puede representar idénticamente por una interacción de un sistema π con dos orbitales p, porque en realidad en el estado de transición lo primero está evolucionando a lo segundo y lo que tendremos será algo intermedio, por tanto dentro del diagrama de interacción ambos son totalmente equivalentes.
Para hacer el diagrama de interacción, aunque hayamos dicho que las interacciones por arriba y por abajo son equivalentes, normalmente lo que se hace es coger las interacciones de tal forma que están siempre por el mismo lado, siempre que eso se corresponda con la topología de la molécula. Entonces antes de empezar a estudiar la interacción entre componentes, lo que hacemos es dentro de cada componente estudiar su interacción, de manera que se produce la interacción siempre por el mismo lado del sistema π, y también teniendo en cuenta que un sistema σ se hace equivalente a la interacción de 2 orbitales.
Si en una reacción pericíclica se postula un estado de transición en el que se puede encontrar un bucle cerrado de orbitales interaccionantes, entonces es lógico pensar que si ese bucle tiene una estructura que recuerde en algo a las de los sistemas aromáticos, este estado de transición estará estabilizado y por tanto la reacción se dará preferentemente frente a otro que esté desestabilizado, porque se parezca a un sistema antiaromático. En este proceso de construcción de estado de transición y su estudio para ver si pueden asociarse a carácter aromático o antiaromático, lo que se hace es la construcción de los diagramas de interacción.
Hemos visto como la interacción se puede definir dentro de los orbitales base de un sistema que interviene en la reacción. Así en un sistema π lineal, se puede establecer la interacción, antes de realizar la reacción, entre los lóbulos de un mismo lado entre si, etc.
A partir de que podemos conocer la interacción que existe dentro de los sistemas que van a intervenir en la reacción, vamos a ver como se define la reacción en el transcurso de la reacción. Hay que tener en cuenta que esa interacción debe de representar la topología de la reacción, por tanto tiene que dar lugar a diagramas de interacción diferentes con topologías diferentes. Teniendo en cuenta que en el transcurso de la reacción los orbitales π y σ se van transformando de forma que en el ET son situaciones intermedias, es por lo que el diagrama de interacción lo podemos transformar desde una interacción σ a dos orbitales p. Lo mismo podemos decir con respecto al diagrama de interacción completo de toda la reacción, de lo que se trata es de reproducir la topología de la reacción teniendo en cuenta que en el ET los orbitales σ no son σ ni los π son π, sino algo intermedio, y lo importante es que reproduzca la topología de como se transforman los reacctivos en los productos pasando por el estado de transición.
Ejemplo de aplicación en reacción Diels-Alder [4+2]
Vamos a poner unos ejemplos para poder establecer unos criterios para dibujar de una forma sencilla estos diagramas de interacción. Supongamos una reacción de cicloadición π2+π4 como la reacción Diels-Alder.
Antes de que se produzca la reacción, podemos definir la interacción dentro de los lóbulos del sistema π de 4 electrones y del sistema π de 2 electrones.

Ahora, podemos decir que esa es una reacción en la que se produce un ataque de un sistema diénico a un sistema etilénico para dar lugar a un sistema cíclico de 6 miembros. Esa interacción puede ser supra–supra o supra–antara. La reacción de Diels-Alder es supra–supra, por tanto se producirá una interacción tal y como está dibujada. Desde interacción para esta reacción, es decir, la representación del estado de transición lo podemos representar de esa manera teniendo en cuenta que da igual que pongamos la interacción por arriba o por abajo, ambas son totalmente equivalentes.

Lo importante es que se produce una interacción de una parte con la otra, de manera que la interacción se produce supra–supra.
Este diagrama de interacción se puede hacer tanto a partir de la reacción directa de cicloadición como de la de cicloreversión. Veamos cómo se obtiene el mismo diagrama para la reacción de cicloreversión. En la cicloreversión tenemos el sistema π y 2 sistemas σ que intervienen, es decir, que en una cicloreversión sería una reacción π2+σ2+σ2. De manera que el diagrama de interacción antes de producirse la reacción sería, teniendo en cuenta que los sistemas σ son equivalentes a los orbitales π.

Esos tres diagramas de interacción son equivalentes, porque en los dos casos tenemos una interacción supra–supra. el diagrama de interacción lo que tiene es que representar el tipo de interacción que se produce.
Ejemplo de interacción en cicloadición [2+2]
Otro ejemplo de interacción supra–supra es el π2+π2 siguiente:

Ahora vamos a ver una interacción supra–antara, vamos a ver que da lugar a una topología totalmente diferente. Supongamos una interacción π2s+π2a, la interacción de los orbitales base antes de dar lugar a la reacción

Esos diagramas de interacción son diferentes de los anteriores, no hay forma de transformar uno en el otro y por tanto implican dos topologías diferentes.
La orientación para que se pueda producir la interacción supra–antara será la siguiente, donde uno de los sistemas se orienta de tal manera que uno de los sistemas π se orienta en un plano perpendicular al plano del papel con el orbital p en el plano del papel. El otro sistema se orienta en una dirección perpendicular de manera que tenemos el sistema π dirigido en un plano perpendicular al plano del papel y por tanto los substituyentes están en el plano del papel.

De manera que el componente que está vertical actúa suprafacialmente, puesto que se va a producir la interacción con los dos lóbulos que van hacia dentro. Pero se puede producir la interacción por arriba y por debajo del otro componente que está en la dirección perpendicular de tal manera que esa interacción se va produciendo y curvándose de tal forma que se produce un retorcimiento que implica un cambio en la configuración de uno de los que actúa de forma antarafacial. Esto implica una topología diferente del acercamiento paralelo de los dos sistemas p que dan lugar al otro diagrama de interacción.
Ejemplo de interacción en transposición sigmatrópica[1,3]
Hemos dibujado unos diagramas de interacción pero no completos, puesto que no hemos dicho nada con respecto a los signos de los lóbulos, ni como se les asigna carácter aromático o antiaromático a esos diagramas de interacción. Antes veremos algunos ejemplos de interacciones pericíclicas donde se puede extraer fácilmente el diagrama de interacción.
Supongamos una reacción de transposición sigmatrópica[1,3]. Donde tenemos un sistema π y un orbital σ que va a transponer desde la posición 1 a la 3. Esta reacción se puede producir de dos formas, una de ellas en la que se produce una interacción supra–supra y otra en la que es supra del sistema π y antara del grupo σ que migra. Para que se produzca una interacción supra–antara tiene que ser de este tipo, donde la representación del estado de transición sería:

Toda la reacción con una interacción supra–antara con el mismo número de electrones tiene que tener el mismo diagrama de interacción.
Ejemplo de interacción en reacción electrocíclica
Veamos un ejemplo de reacciones electrocíclicas, por ejemplo la apertura conrotatoria o disrotatoria. Si la apertura es conrotatoria, la interacción es supra–antara y tiene que dar un diagrama de interacción similar al que hemos visto antes de la reacción de transposición sigmatrópica o a la cicloadición π2s+π2a.

Ya hemos visto que la apertura conrotatoria implica una cicloadición π2a+σ2s.
La disrotatoria tiran en sentido conrotatorio y por tanto un lóbulo va hacia arriba y el otro también.

Lo cual es totalmente equivalente a una cicloadición π2s+π2s. Así en general, seremos capaces de dibujar cualquier diagrama de interacción de cualquiera de las reacciones que hemos dicho hasta ahora. Simplemente, teniendo en cuenta la topología de la reacción y las interacciones supra o antara que se producen en los distintos componentes u orbitales base que intervienen en la reacción.
Carácter aromático/antiaromático en los diagramas de interacción
Una vez que sabemos construir el diagrama de interacción veamos como se le asignan los caracteres aromáticos o antiaromáticos a estos diagramas, para lo cual tenemos que ponerles signos a los lóbulos de los orbitales p que integran el diagrama de interacción. La norma que se sigue es + para los lóbulos que estén unidos por líneas de interacción siempre que sea posible.

Vemos como en el segundo caso no podemos asignarle el signo + a todos los lóbulos unidos. Por tanto vemos como la topología del diagrama de interacción implica que todas las interacciones se hacen entre lóbulos positivos en el primer caso mientras que en el segundo se producen entre lóbulos que tienen distinto signo.
Pero en general la asignación de signos se puede hacer de forma aleatoria, por ejemplo, en el primer caso anterior.
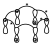
Inversión de fase
Cuando se asignan los signos, se dice que se produce una inversión de fase, si existe una interacción entre lóbulos de distinto signo. En ese diagrama por lo tanto habrá 4 inversiones de fase. En el caso de las 2 anteriores, en el primero había cero inversiones de fase y en el segundo caso había una.
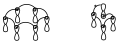
Si en uno de esos diagramas cambiamos algún signo de sitio, en el primer caso al cambiar signos de sitio de forma aleatoria aparece un número par de inversiones de fase y en cambio en el segundo caso aparece un número impar de inversiones de fase.

En general cuando existe una topología supra–supra entre todos los componentes se obtienen diagramas de interacción con un número par (o cero) de inversiones de fase. Mientras que cuando la interacción es supra–antara estos diagramas tienen número impar de inversiones de fase o como mínimo una. Siempre podremos reducir los diagramas de interacción al número mínimo de inversiones de fase (0 ó 1).
Ahora ya estamos en condiciones de definir si un diagrama de interacción será aromático o antiaromático, por analogía a los sistemas conjugados. Así, en el benceno y en el ciclobutadieno tenemos:

Para el benceno tenemos 6 electrones y la interacción que hay es una en la que todos los lóbulos de arriba interaccionan entre si (con 0 inversiones de fase). En el caso del ciclobutadieno también se puede representar como una interacción supra–supra con 4 electrones. Entonces los sistemas con número de electrones π = 4n+2 (n=1, 2, 3, …) son aromáticos, y los sistemas cíclicos (saturados) conjugados con un número de electrones π = 2n son antiaromáticos. Pero tanto unos como otros responden a diagramas de interacción con cero inversiones de fase. Los sistemas aromáticos están estabilizados frente a los sistemas conjugados no cíclicos mientras que los antiaromáticos están desestabilizados.
Sistemas Hückel y Möbius
Hay sistemas conjugados grandes en los que se produce un retorcimiento en la cadena mediante lo que se llama cintas de Möbius. Sin embargo un sistema aromático lo podemos representar como un círculo en donde siempre se produce una interacción por arriba y por abajo. Mientras que en un sistema de Möbius se produce un plegamiento de tal manera que la parte de arriba termina interaccionando con la parte de abajo.

Esto hace que el carácter aromático o antiaromático en un sistema policíclico cambie. En un sistema de Möbius el carácter aromático se asocia con un número de electrones igual a 4n, mientras que el carácter antiaromático se asocia con un número de electrones igual a 4n+2. Además, la interacción implica una inversión de fase porque se produce un plegamiento. Dicho esto podemos asignar el carácter aromático o antiaromático a los diagramas de interacción. Por tanto los dividiremos en dos grupos:
Diagramas de interacción con 0 inversiones de fase
Se les conoce como anillos tipo Hückel. En estos diagramas se les asigna un carácter aromático a aquellos que poseen un número de electrones igual a 4n+2, a los que tiene 4n se les asigna carácter antiaromático. Los primeros están favorecidos frente a los segundos, en ellos el estado de transición estará estabilizado, por tanto los primeros se darán con mayor facilidad. Se dice que los que tienen carácter aromático están permitidos, mientras lo que son antiaromáticos están prohibidos (no significa que no se puedan dar, sino que existe una barrera energética en el estado de transición muy grande, pero en condiciones especiales podrían darse el prohibido y no el permitido (por ej. interacciones estéricas).
Diagramas de interacción con 1 inversión de fase
Se definen también anillos de tipo anti-Hückel o diagramas de interacción de tipo anti-Hückel, como aquellos que tienen una inversión de fase. En estos casos se le asocia carácter aromático a aquellos diagramas de interacción que tienen un número de electrones igual a 4n, mientras que serán antiaromáticos los que tengan un número 4n+2.
Entonces para predecir si una reacción se dará o no, se reduce a construir el diagrama de interacción, una vez que lo hagamos vemos si corresponde a una o cero inversiones de fase, vemos el número de electrones del diagrama y podemos decir si es permitida o prohibida.
Supongamos las reacciones electrocíclicas, donde se produce la apertura de ese orbital σ (o cierre, puesto que es una reacción reversible) para dar lugar al trieno correspondiente. La apertura como sabemos puede ser conrotatoria o disrotatoria.

Si es disrotatoria, tendremos por una parte el sistema π de 4 electrones que interaccionan con el sistema s de dos electrones, de manera que el sistema s se abrirá hacia arriba los dos de manera que se producirá la interacción por arriba y tendremos una interacción supra–supra, lo cual implica cero inversiones de fase y como hay 6 electrones será un sistema aromático y esa reacción estará permitida. La apertura electrocíclica con 6 electrones será permitida si es distrotatoria:

En la conrotatoria en cambio se produce el giro de un lóbulo hacia arriba y otro hacia abajo, por lo que la interacción se producirá con una inversión de fase, será un anillo anti-Hückel y por tanto la reacción estará prohibida ya que es un sistema antiaromático.

Esto implica que este último estado de transición tiene una energía de activación mucho mayor que el anterior y la reacción se dará preferentemente por el primer camino.
Veamos ahora otras aproximaciones, puesto que lo que queremos es predecir cuando una reacción se dará y con qué estereoquímica.
Interacciones de orbitales frontera
Esta aproximación fue propuesta por Woodward-Hoffmann y desarrollada posteriormente por Fukui. Se denominan orbitales frontera al HOMO y LUMO.
Según la teoría de perturbaciones, para que una interacción se produzca lo más favorablemente posible, tiene que realizarse entre un orbital lleno y otro vacío, y además, que los dos orbitales tengan un contenido energético lo más favorable posible. Esto es algo que se cumple con los orbitales frontera. Puesto que si tenemos una serie de orbitales podrían, en principio, interaccionar cualquier orbital ocupado con otro vacío, pero la gran diferencia de energía entre ellos será muy grande. Sin embargo, la diferencia es pequeña cuando interaccionan el último de los ocupados (HOMO) con el primero de los desocupados (LUMO). Estas serán las condiciones preferidas para que se dé lo mejor posible una interacción entre orbitales.
Además, Woodward-Hoffmann propusieron que para que se pueda producir una interacción entre dos orbitales tienen que tener la misma simetría. Por tanto, de todas las posibilidades que hubiera se darán sólo aquellas que tengan la misma simetría entre los orbitales interaccionantes. De esta manera, se pueden racionalizar las distintas reacciones pericíclicas.
Ejemplo se cicloadición [2+2]
Por ejemplo, supongamos una cicloadición π2 + π2. En esta reacción podemos tener dos elementos de simetría, consideremos el elemento de simetría que bisecta a ambos sistemas (plano σ). Con respecto a ese plano se consideran los orbitales de los sistemas interaccionantes. Por una parte en uno de los sistemas tenemos el orbital π enlazante y otro π*, e igual para el otro sistema.

La simetría se toma con respecto a ese plano. Si ahora la interacción se tiene que producir entre el LUMO de uno y el HOMO de otro, pero como no tienen simetría adecuada, esa reacción estará prohibida por simetría. La única posibilidad es que se produzca interacción entre los dos HOMOs o los dos LUMOs. El primero da lugar a dos orbitales ocupados y esto es una situación desestabilizante y el segunda da lugar a dos vacíos virtuales que par tanto no sirve de nada.
Ejemplo de cicloadición [4+2]
Si ahora consideramos una cicloadición π4 + π2. En el sistema π4 tendremos cuatro orbitales de los cuales los dos primeros están ocupados y los dos siguientes son virtuales, la simetría con respecto al mismo plano que sigue siendo el elemento de simetría será:

Como se ve, ahora si se puede establecer la interacción entre el HOMO del etileno y el LUMO del butadieno, dando lugar a una interacción estabilizante puesto que se puebla el orbital de más baja energía. Además se puede dar entre el HOMO del butadieno y el LUMO del etileno donde también se puebla el orbital de más baja energía. Por tanto se pueden producir dos interacciones igualmente estabilizantes (aunque no serán muy estabilizantes puesto que el solapamiento es pequeño, pero lo suficiente como para que se produzca un descenso de energía).
Lo normal es que el sistema diénico tengo un substituyente electrón donante y el sistema etilénico electrón atrayente, con esto lo único que se consigue es que las diferencias de energía que aquí son idénticas para ambas interacciones, una de ellas salga muy estabilizada frente a otra aunque sólo se produzca una interacción entre el HOMO del dador con el LUMO del aceptor, de las dos posibles interacciones que se pueden dar.